Pakatavad rahasalved ehk jää ja vee struktuur

Carl Barksi klassikalises koomiksis „Suur rahasalv Seisaku mäel“ [1] täidab Onu Robert, järgides Piilupart Donaldi nõuannet, oma rahasalve veega, et seda Penipoiste eest kaitsta. Kahjuks juhtub see olema üks Pardilinna külmemaid öid. Vesi jäätub ja lõhub varasalve kolme meetri paksused seinad. Selle tulemusel pääseb valla hiiglaslik rahaga täidetud jääkamakas, mis libiseb mäest alla otse Penipoiste hoovi.

Franco Bagnoli (franco.bagnoli@unifi.it – DOI: 10.1051/epn/2015301, Füüsika ja astronoomia osakond ning kompleksse dünaamika teaduskeskus Firenze Ülikool, Itaalia – Via G. Sansone, 150019 Sesto Fiorentino (FI) Itaalia

Jäätuva vee paisumine on kõigile teada-tuntud fakt. Just see nähtus põhjustab sügavkülma jäetud õllepudelitega tihti palju pahandust. Aga miks vesi niimoodi käitub? Ja mis veel keerulisem, kuidas seda nähtust lihtsalt ja arusaadavalt selgitada?

Kõigepealt tuleb meeles pidada, et temperatuur on seotud molekulide kineetilise energiaga. Molekulid aga eelistavad püsida miinimumenergia seisundis. Kui võtta aluseks lihtne palli mudel, siis on aatomid miinimumenergia seisundis paigutunud kompaktsemalt kui rohkem energiat nõudvas (korrapäratus) struktuuris. See seaduspärasus ei kehti vee puhul.

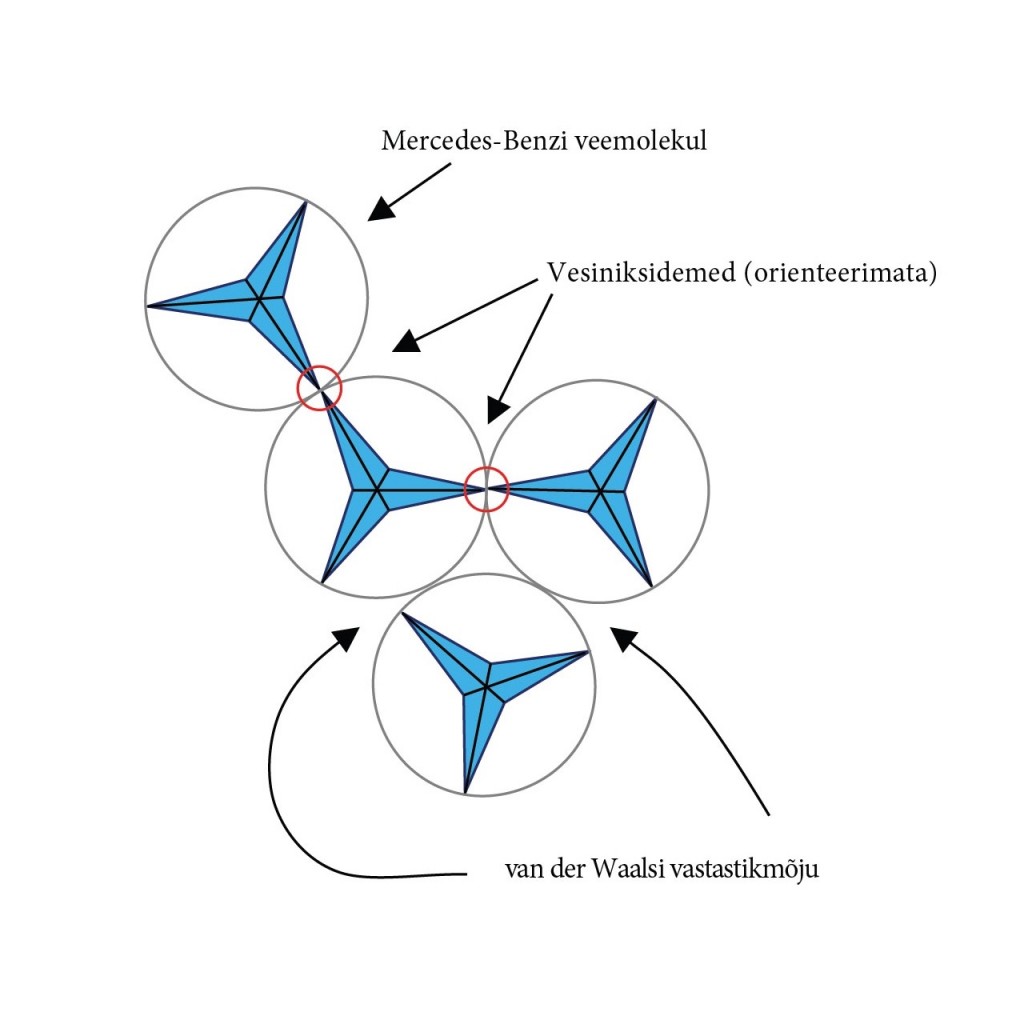
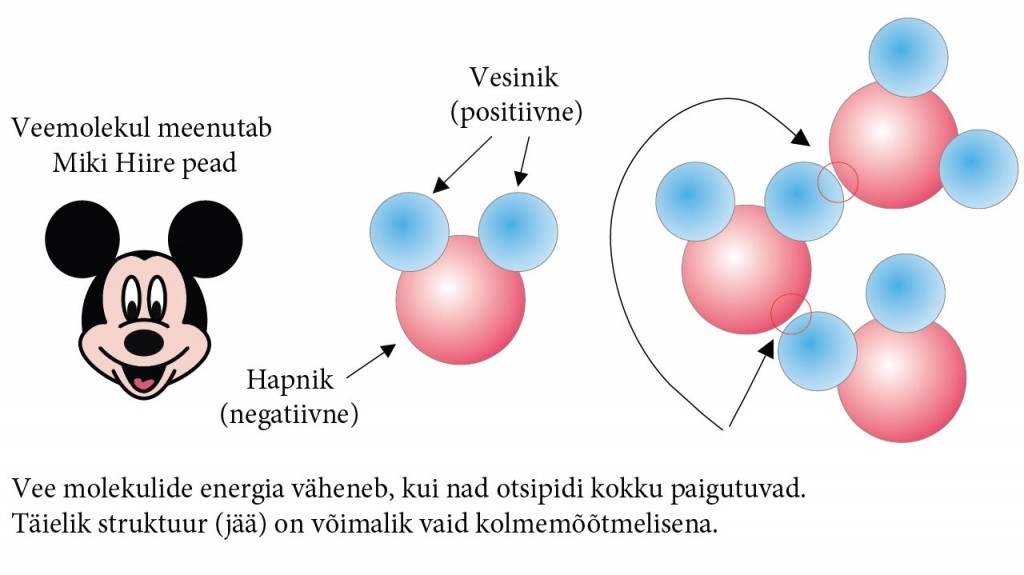
Veemolekulid meenutavad kujult Miki Hiire pead (vt joonis 1), kellel on kõrvadeks kaks vesinikuaatomit. Et vee kristalli struktuur on olemuselt kolmemõõtmeline, on seda keeruline joonistada. Siinkohal on hea kasutada Mercedes-Benzi mudelit [2].

Selles mudelis kujutatakse veemolekule kuulsa Mercedes-Benzi sümbolina (vt joonis 2) ning miinimumenergia seisund saavutatakse kahe teraviku ühinemisel (suunamata vesinikside). Mercedes-Benzi molekule on üsna lihtne papist valmistada, et inimesed saaks nendega nähtuse läbi mängida.

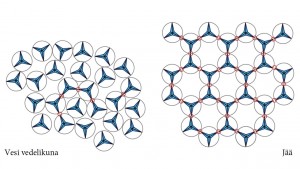
Selle mudeli abil on kerge selgitada miinimumenergia seisundiga kaasnevat tühimikku jää struktuuris (vt joonis 3, parempoolne osa) ja põhjendada jää väiksemat tihedust veega võrreldes. Samuti võib selle abil näitlikustada taasjäätumise nähtust (jää sulab rõhu all ja jäätub uuesti, kui rõhku vähendada). Püsiva jää struktuuri saamiseks tuleb kõigepealt vähendada veemolekulide kineetilist energiat. Seejärel tuleb ületada van der Waalsi jõust tulenva seose ja vesiniksideme energeetiline erinevus, st soojus peab eralduma. Makrokäsitluses nimetatakse esimest vee soojusmahtuvuseks (vee erisoojus: c = 4,187 kJ/kg·K) ja teist jää sulamissoojuseks (λ = 334 kJ/kg). Kui tahta veel jää temperatuuri alandada, tuleb eraldada energiakogus, mis vastab jää erisoojusele (2,108 kJ/kg·K).

Carl Barksi koomiksis ütleb Onu Robert korduvalt, et tema rahasalve maht on kolm kuupaakrit, mis ilmselgelt ei vasta tõele, sest aaker on pindala ühik. Kui oletada, et kuubi iga külg on aakri suurune (umbes 4000 m²), on serv umbes 60 m ja maht V ligikaudu 200 000 m³. Mul ei õnnestunud leida andmeid korrapäratult pakitud müntide kohta (paistab, et selles valdkonnas on uuritud ainult kerasid ja M&Mi komme [3]), seega tegin ma ise 174 kümnesendise mündiga väikse katse. Pakkimistiheduse tulemus oli umbes 0,55, mis on palju väiksem kui keradel (0,64), kuid näha on piiratud ruumala mõju¹. Seega on vee koguhulk m = 0,45·2·10⁵·10³ = 9·10⁷kg. Oletades, et algul on rahasalv (ja selles olev vesi) temperatuuril t = 10°C, tuleb 0°C temperatuuriga jää saamiseks eraldada soojushulk m·(c·t+k) = 3,4·10¹³ J. Arvestamata jääb müntide soojusmahtuvus (vasel või messingil vaid 0,4 kJ/kg·K) ja seinte soojusmahtuvus (umbes 0,8 kJ/kg·K). Kui jäätumine toimub näiteks 5 tunni jooksul, on jahutusvõimsus umbes 2 GW! Vee külmutamine pole tõepoolest kerge ülesanne. Seetõttu pannaksegi viljapuude lähedusse veetünnid, et neid külma eest kaitsta. Lõpetame nuputamisülesandega: milline on veetemperatuur merepõhjas?²

Viited

[1]   http://coa.inducks.org/story.php?c=W+WDC+135-02 (1951). Internetis kättesaadav leheküljel http://it.paperpedia.wikia.com/wiki/File:-Big_bin_on_killmotor_hill.pdf

[2]   K.A.T. Silverstein, A.D.J. Haymet, K.A. Dill, J. Am. Chem. Soc. 120, 3166 (1998).

[3]   A. Donev, I. Cisse, D. Sachs, E.A. Varano, F.H. Stillinger, R. Connelly, S. Torquato, P.M. Chaikin, Science 303, 990 (2004).

¹Selle abil saame välja arvutada, kui rikas on Onu Robert. Ühedollarilise mündi maht on umbes 1,1 cm³ ja pakkimistiheduse 0,55 juures võtab see enda alla ligikaudu 2 cm³. Jagades V selle arvuga, saame tulemuseks umbes 10¹¹ dollarit, sada tuhat miljonit ehk sada miljardit.

²Analüüsime seda olukorda kõigepealt magevee tingimustes (sügava järve puhul). Meie mudeli järgi on vee tihedus suurim temperatuuril veidi üle nulli (reaalsel puhtal veel on see umbes 4°C). Madalamal temperatuuril tekivad vees tihti jääsarnased struktuurid, kus on rohkelt vesiniksidemeid. Need muudavad tiheduse väiksemaks, jää tiheduse suunas. Kõrgema temperatuuri korral domineerivad van der Waalsi jõud ja vesi käitub rohkem tavavedeliku moodi. Soolasisaldus veidi muudab olukorda, tahkumistemperatuur on seal madalam ja vee maksimumtihedus samuti väiksem. Seega on ookeanipõhjas veetemperatuur umbes 3°C.

Artikkel on originaalis saadaval aadressil http://www.europhysicsnews.org või http://dx.doi.org/10.1051/epn/2015301